
Interferometry is a family of techniques in which waves, usually electromagnetic waves, are superimposed causing the phenomenon of interference in order to extract information.[1] Interferometry is an important investigative technique in the fields of astronomy, fiber optics, engineering metrology, optical metrology, oceanography, seismology, spectroscopy (and its applications to chemistry), quantum mechanics, nuclear and particle physics, plasma physics, remote sensing, biomolecular interactions, surface profiling, microfluidics, mechanical stress/strain measurement, velocimetry, and optometry.[2]:1–2
Interferometers are widely used in science and industry for the measurement of small displacements, refractive index changes and surface irregularities. In an interferometer, light from a single source is split into two beams that travel different optical paths, then combined again to produce interference. The resulting interference fringes give information about the difference in optical path length. In analytical science, interferometers are used to measure lengths and the shape of optical components with nanometer precision; they are the highest precision length measuring instruments existing. In Fourier transform spectroscopy they are used to analyze light containing features of absorption or emission associated with a substance or mixture. An astronomical interferometer consists of two or more separate telescopes that combine their signals, offering a resolution equivalent to that of a telescope of diameter equal to the largest separation between its individual elements.
Basic principles

Figure 2. Formation of fringes in a Michelson interferometer
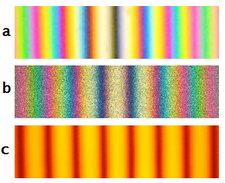
Figure 3. Colored and monochromatic fringes in a Michelson
interferometer: (a) White light fringes where the two beams differ in
the number of phase inversions; (b) White light fringes where the two
beams have experienced the same number of phase inversions; (c) Fringe
pattern using monochromatic light (sodium D lines)
Typically (see Fig. 1, the well-known Michelson configuration) a single incoming beam of coherent light will be split into two identical beams by a beam splitter (a partially reflecting mirror). Each of these beams travels a different route, called a path, and they are recombined before arriving at a detector. The path difference, the difference in the distance traveled by each beam, creates a phase difference between them. It is this introduced phase difference that creates the interference pattern between the initially identical waves.[2]:14–17 If a single beam has been split along two paths, then the phase difference is diagnostic of anything that changes the phase along the paths. This could be a physical change in the path length itself or a change in the refractive index along the path.[2]:93–103
As seen in Fig. 2a and 2b, the observer has a direct view of mirror M1 seen through the beam splitter, and sees a reflected image M'2 of mirror M2. The fringes can be interpreted as the result of interference between light coming from the two virtual images S'1 and S'2 of the original source S. The characteristics of the interference pattern depend on the nature of the light source and the precise orientation of the mirrors and beam splitter. In Fig. 2a, the optical elements are oriented so that S'1 and S'2 are in line with the observer, and the resulting interference pattern consists of circles centered on the normal to M1 and M'2. If, as in Fig. 2b, M1 and M'2 are tilted with respect to each other, the interference fringes will generally take the shape of conic sections (hyperbolas), but if M1 and M'2 overlap, the fringes near the axis will be straight, parallel, and equally spaced. If S is an extended source rather than a point source as illustrated, the fringes of Fig. 2a must be observed with a telescope set at infinity, while the fringes of Fig. 2b will be localized on the mirrors.[2]:17
Use of white light will result in a pattern of colored fringes (see Fig. 3).[2]:26 The central fringe representing equal path length may be light or dark depending on the number of phase inversions experienced by the two beams as they traverse the optical system.[2]:26,171–172 (See Michelson interferometer for a discussion of this.)




0 Comments